樸素的多項式乘法,必須在 \(O(n^2)\) 完成。
我們可以透過 FFT 的協助,在 \(O(nlogn)\) 時間內完成多項式乘法。
點值表達式
可以帶入至少 \(n\) 個點來唯一表示 \(n-1\) 次多項式。
所以,\(n > deg\ f(x)\),\(f(x)\) 能以點值表達式表示為
\[(x_0,f(x_0)), (x_1,f(x_1)), \dots, (x_{n-1},f(x_{n-1}))\]
兩個點值表達式的乘法可以在 \(O(n)\) 達成,\((fg)(x)\) 可以被表示為:
\[(x_0,f(x_0)g(x_0)), (x_1,f(x_1)g(x_1)), \dots, (x_{n-1},f(x_{n-1})g(x_{n-1}))\]
記得取 \(n > deg\ (fg)(x)\)
因此對於多項式乘法,我們有了計畫:
係數表達式 \(\rightarrow\) 點值表達式 \(\rightarrow\) \(O(n)\) 相乘 \(\rightarrow\) 點值表達式 \(\rightarrow\) 係數表達式
我們的瓶頸將會在,如何快速的做到係數表達式轉換點值表達式
FFT
定義一個函數 \(FFT\),傳入 \(X_0, X_1, \dots, X_{n-1}\) 和 \(n\) 個係數 \(P_0, P_1, \dots, P_{n-1}\),可以計算出帶入 \(X\) 的結果是多少。
\[ FFT(X,P) = \begin{bmatrix} X_0^0 & X_0^1 & \dots & X_0^{n-1}\\ X_1^0 & X_1^1 & \dots & X_1^{n-1}\\ \vdots & \vdots & \ddots & \vdots \\ X_{n-1}^0 & X_{n-1}^{1} & \dots & X_{n-1}^{n-1} \end{bmatrix} \begin{bmatrix} P_0\\ P_1\\ \vdots\\ P_{n-1}\\ \end{bmatrix} = \begin{bmatrix} f(X_0)\\ f(X_1)\\ \vdots\\ f(X_{n-1})\\ \end{bmatrix}\]
為了減少計算量,我們可以利用偶函數的性質:\(f(x) = f(-x)\),只要帶入一個數字就能得到兩份結果:
\[ \begin{aligned} f(x) & = p_0x^0 + p_1x^1 + \dots + p_{n-1}x^{n-1}\\\\ & = (p_0x^0 + p_2x^2 + \dots + p_{n-2}^{n-2}) + x(p_1x^1 + p_3x^2 + \dots + p_{n-1}^{n-2}) \end{aligned}\]
為了更方便觀察出遞迴的性質,以及 \(f(x)\) 和 \(f(-x)\) 的關係,可以這樣表示:
\[ \begin{aligned} &f(x) = f_e(x^2) + xf_o(x^2)\\ &f(-x) = f_e(x) -xf_o(x^2)\\ &f_e(x) = p_0x^0 + p_2x^2 + \dots + p_{n-2}x^{\frac n 2 -1}\\ &f_o(x) = p_1x^0 + p_3x^2 + \dots + p_{n-1}x^{\frac n 2 -1}\\ \end{aligned} \]
現在,只要算出 \(f(x)\) 就能順便得到 \(f(-x)\)。把後半的 \(X\) 皆對應到前半的 \(X\),使他們互為相反數:
\[ X_i = X_{i+\frac n 2}, i<\frac n 2 \]
這樣就有了 \(FFT\) 函數的轉移,大概長這樣:
\[ FFT(X,P) = merge( FFT(X_{half},P_{even}),\ FFT(X_{half},P_{odd})) \]
\[ X_{half} = [X_0, X_1, \dots, X_{\frac n 2-1}] \\ P_{even} = [P_0, P_2, \dots, P_{n-2}] \\ P_{odd} = [P_1, P_3, \dots, P_{n-1}] \\ \]
\(merge\) 的地方,就是第 \(i\) 項相加得到 \(f(X_i)\),相減得到 \(f(X_{i+\frac n 2})\)
接著需要處理,\(X\) 裡面究竟該放什麼,才能順利的遞迴下去。考慮:
\[ X = [a_0, a_1, \dots, a_{n-1}] \]
遞迴下去會變成:
\[ [a_0^2, a_1^2, \dots, a_{\frac n 2 -1}^2] \]
我們需要在遞迴的每一層都保證後半部是前半部的相反數,也就是 \(X_i = X_{i+\frac n 2}, i<\frac n 2\)。
只考慮實數是不可能的,因為下一層是上一層的平方,不會是相反數。
單位複根
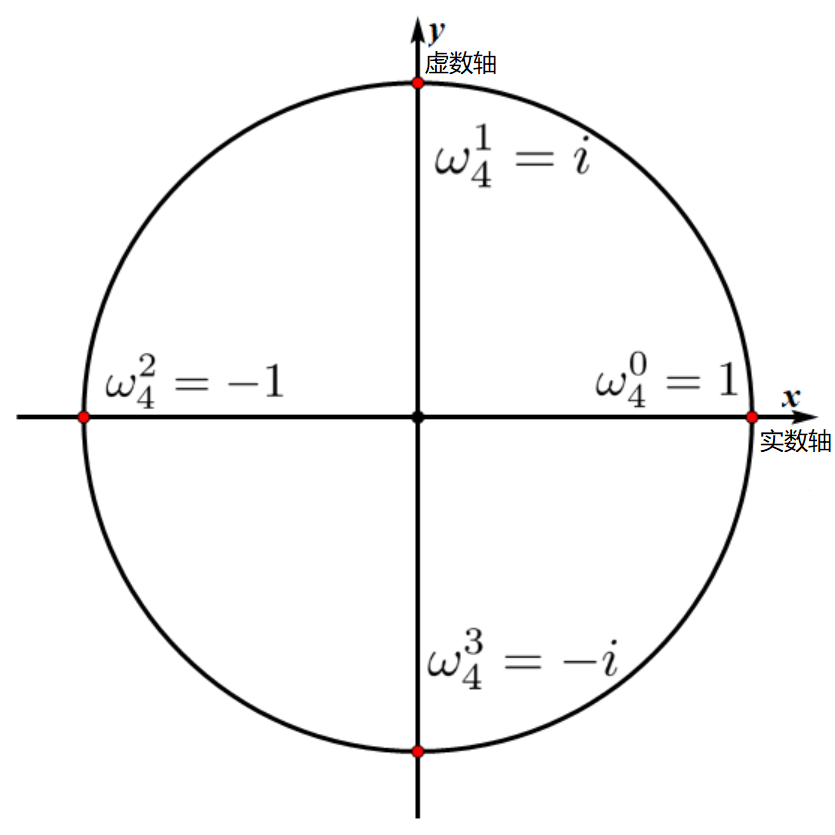
定義 \(\omega_n^i\) 為 \(x^n=1\) 下的其中一個解,這樣的解有 \(n\) 個,把單位圓等分,且有以下性質我們會用到的性質:
\[ \omega_n^i = \omega_n^{i+\frac n 2}\\ (\omega_n^i)^2 = \omega_{\frac n 2}^i \]
這兩個性質用n次單位根等分單位圓、複數相乘幅角相加可以說明
直接取 \(X_i = \omega_n^i\),單位根的性質恰好符合我們的要求:保持後半部是前半部的相反數
遞迴下去之後,\(X = [\omega_{\frac n 2}^0, \omega_{\frac n 2}^1, \dots, \omega_{\frac n 2}^{\frac n 2 -1}]\),依舊保證了這件事。
Inverse FFT
前面有提到 FFT 可以看成矩陣相乘的過程,那個 \(n \times n\) 的矩陣我們叫他 \(DFT\) 矩陣。
從點值找出係數的過程,就是左右乘上 \(DFT^{-1}\),而 \(DFT^{-1}\) 長這樣:
\[ \begin{bmatrix} \omega_0^0 & \omega_0^{-1} & \dots & \omega_0^{-(n-1)}\\ \omega_1^0 & \omega_1^{-1} & \dots & \omega_1^{-(n-1)}\\ \vdots & \vdots & \ddots & \vdots\\ \omega_{n-1}^0 & \omega_{n-1}^{-1} & \dots & \omega_{n-1}^{-(n-1)}\\ \end{bmatrix} \]
就是每個元素都倒數,原因我不是很清楚。
實作
\[ \omega_n^k = cos \frac{2 \pi k}{n}i + sin \frac{2 \pi k}{n}i \]
這很容易在複數平面上看端倪。
實作時就用這個公式及 C++ 內建的 Complex 處理即可。